If the Order Quantity Doubles What Happens to the Frequency of Orders

Inventory control features in the syllabuses of several ACCA exams. The areas ordinarily tested in these exams are:

• determining an economic guild quantity (EOQ) – calculations to assess how many units of a item inventory particular to order at a time
• finding an optimal re-order level (optimal ROL) – providing some idea of the level to which inventories tin be immune to autumn earlier placing an order for more than
• discussions of various practical aspects of inventory management – often referred to by students with no applied experience as 'theory'.

Advantages and disadvantages of holding inventory

The basis of the theoretical calculations of an EOQ and an optimal ROL is that there are advantages and disadvantages of holding inventory (of buying inventory in large or minor quantities). The advantages include:

• the demand to meet customer demand
• taking reward of bulk discounts
• reducing full annual re-ordering cost

The disadvantages include:

• storage costs
• cost of capital letter tied up in inventory
• deterioration, obsolescence, and theft

The aim behind the calculations of EOQ and ROL is to weigh up these; and other advantages and disadvantages and to observe a suitable compromise level.

EOQ

When determining how much to order at a time, an organisation will recognise that:

• as lodge quantity rises, average inventory rises and the total annual cost of belongings inventory rises
• as order quantity rises, the number of orders decreases and the full annual re-order costs decrease.

The total of annual property and re-lodge costs first decreases, then increases. The point at which cost is minimised is the EOQ. This cost behaviour is illustrated by the graph in Figure i.

Effigy ane

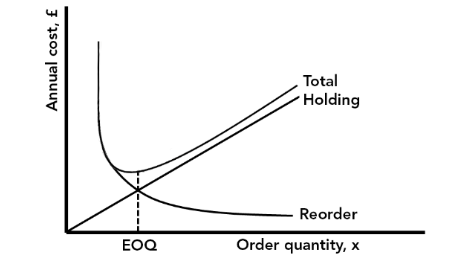
The fashion in which this EOQ is calculated is based on sure assumptions, including:

• abiding purchase price
• constant demand and abiding lead-fourth dimension
• belongings-toll dependent on average inventory
• order costs contained of guild quantity

The assumptions effect in a blueprint of inventory that can be illustrated graphically as shown in Figure 2.

Figure 2

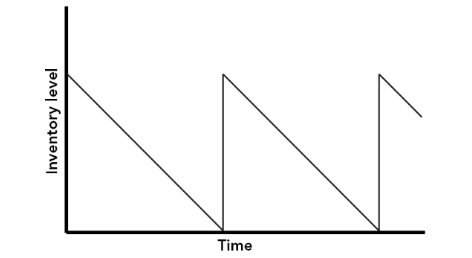
The formula

Using the standard ACCA notation in which:
CH = cost of property a unit of measurement of inventory for a yr
CO = cost of placing an order
D = annual demand

also:
TOC = total annual re-ordering cost
THC = total almanac property toll
Q = order quantity

then:
average inventory = Q/2

THC = Q/two × CH

and:
number of orders in a twelvemonth = D/Q

TOC = D/Q × CO

The full almanac toll (affected by order quantity) is:
C = THC + TOC = Q/2 × CH + D/Q × CO

This formula is not supplied in exams – it needs to be understood (and remembered).

The value of Q, order quantity, that minimises this total price is the EOQ, given by an easily remembered formula:

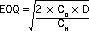
Utilise of EOQ Formula

You need to take care over which figures you put into the formula, particularly in multiple-choice questions. The areas to beware of autumn into two categories:

1. Relevant costs – only include those costs affected past order quantity. But include those holding costs which (in total in a year) will double if yous order twice equally much at a time. (Thus, fixed salaries to storekeepers or buying department staff will be excluded.)
2. Consistent units – ensure that figures inserted have consistent units. Almanac demand and cost of holding a unit of measurement for a year. Both holding costs and re-ordering costs should exist in $, or both in cents.

Bulk Discounts

A common twist to exam questions is to ask students to evaluate whether bulk discounts are worth taking. While prices reduce, total annual belongings costs will increase if more inventory is ordered at a fourth dimension, and so the matter needs a trivial thought.

The common approach is ane of trial and mistake. This involves finding the total annual toll (holding cost, re-ordering cost and purchasing price) at the level indicated by the EOQ and at the level(s) where discount first becomes available.
Figure iii shows total costs (now including cost of purchasing the inventory) plotted confronting order quantity with disbelieve incorporated.

Effigy 3

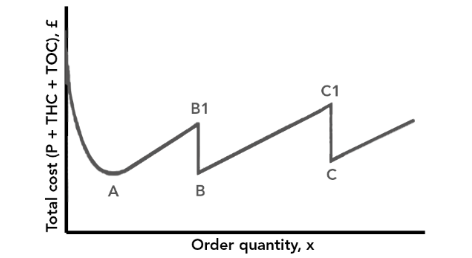
Bespeak A represents the toll at the order quantity indicated by the EOQ. If inventory is ordered in larger quantities, total costs will increase to bespeak B1, at which stage bulk discounts are available, bringing the costs downward to point B. Any calculations volition involve finding which cost out of A, B or C is the everyman, every bit Example one will show.

Example i
Moore Limited uses five,000 units of its main raw material per month. The material costs $4 per unit to buy, supplier's delivery costs are $25 per guild and internal ordering costs are $two per order. Total annual holding costs are $1 per unit. The supplier has offered a discount of 1% if 4,000 units of the textile are bought at a time.

Required:

1. Plant the economic society quantity (EOQ) ignoring the discount opportunities.
2. Make up one's mind if the discount offer should exist accepted.
   

Example 1 solutions

Re-club levels

Every bit important equally how much to society at a time is the question of when to order more inventory. If an order is placed too late, when inventories have been immune to run too depression, a 'stock-out' will occur, resulting in either a loss of production or loss of sales, or possibly both.

If orders are placed too before long, when at that place are nonetheless substantial supplies in inventory, and so inventory levels and holding costs will be unnecessarily loftier. The re-gild level equally explained below should not be confused with the inventory command levels referred to in textbooks – this article ignores these. When information technology comes to computing re-order levels, three sets of circumstances tin be envisaged.

Lead-fourth dimension is cipher

'Lead-time' is the interval between placing an order with a supplier and that gild arriving. It is unlikely that this could be reduced to nada – it would require astonishingly branch and efficient suppliers. If it were possible, a re-gild level of zero could be adopted. An organisation could simply wait until it ran out of inventory, click its corporate fingers, and inventory would arrive instantaneously.

Constant need, fixed finite lead-time

The assumption of constant demand is consistent with the assumptions underlying the EOQ formula. If suppliers take some time to provide goods, orders need to exist placed in advance of running out. Figure 4 illustrates the problem and its solution.

Figure 4

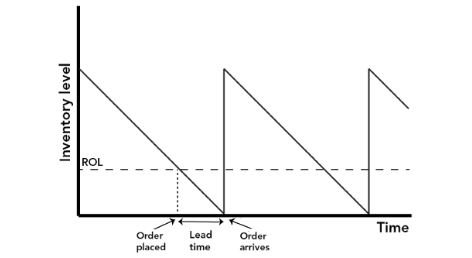
If the pb-fourth dimension is, say, five days, an order has to be placed earlier inventories accept been exhausted. Specifically, the society should be placed when at that place is still sufficient inventory to last 5 days, ie:

Re-society level (ROL) = Demand in lead-time

And then, if lead-time for a particular inventory item is v days and daily demand is 30 units, the re-order level would be five days at thirty units per twenty-four hour period, 150 units.

Variable demand in the lead-fourth dimension

If need in lead-time varied, it could be described by means of some form of probability distribution. Taking the previous case of the demand in pb-time existence 150 units, we're because the possibility of need beingness more than than 150 or less than that.

Note: This aspect of inventory command produces a few issues. The EOQ formula requires that need (and lead-time) for a inventory item be constant. Here the possibility of need varying or pb-time varying or both varying is introduced. Setting that problem aside, most ACCA syllabuses at the lower levels avoid any discussion of uncertainty or probability distributions. All the same, dubiousness in atomic number 82-time need in inventory control has featured in exams.

In these circumstances, a business firm could identify an order with a supplier when the inventory brutal to 150 units (the average demand in the atomic number 82-time). All the same, there'south a 33% chance (0.23 + 0.08 + 0.02 = 0.33) that demand would exceed this re-guild level, and the organisation would exist left with a trouble. It is therefore advisable to increment the re-order level by an amount of 'buffer inventory' (condom inventory).

Buffer inventory

Buffer inventory is simply the amount past which ROL exceeds average need in lead-time. It is needed when at that place is uncertainty in atomic number 82-time demand to reduce the chance of running out of inventory and reduce the cost of such shortages.

If a ROL of 160 units was adopted, this would correspond to a buffer inventory of 10 units (and reduce the hazard of running out of inventory to 0.08 + 0.02 = 0.i, or x%). A ROL of 170 is equivalent to a buffer inventory of 20 and reduces the run a risk of running out to 2%, and a ROL of 180 implies 30 units of buffer inventory (and no take chances of running curt).

Optimal Re-order Levels

This leaves the problem of how to calculate the optimal ROL. At that place are two common means in which one could determine a suitable re-society level (if the information was available):

1. A tabular arroyo – Calculate, for each possible ROL (each level of buffer inventory) the cost of property different levels of buffer inventory and the cost incurred if the buffer is inadequate ('stock-out' costs). The optimal re-order level is that level at which the total of holding and stock-out costs are a minimum.
2. A 'service level' approach – An organisation has to determine a suitable level of service (an acceptably pocket-size probability that it would run out of inventory), and would demand to know the nature of the probability distribution for lead-fourth dimension need. These 2 would be used to find a suitable ROL.

Written by a member of the direction accounting examining team

lussierinds1974.blogspot.com

Source: https://www.accaglobal.com/gb/en/student/exam-support-resources/fundamentals-exams-study-resources/f2/technical-articles/stock-control.html

Share this post